- раздел физики, посвящённый изучению ядерных процессов, в к-рых частицы,
составляющие ядерную материю, движутся со скоростями, близкими к скорости
света с. Р. я. ф. сформировалась в 1970-72 в связи с экспериментами на
пучках релятивистских ядер, полученных на синхрофазотроне ОИЯИ (Дубна, СССР)
н на бетатроне (Беркли, США). Как составляющая часть первичного космич.
излучения релятивистские ядра наблюдались с 1948 в космич. лучах.
Пусть I и II - сталкивающиеся ядра (AI, АII- массовые числа), а 1, 2, 3,...-
продукты реакции ( А1, А2, А3):
Эксперим. методики позволяют определить импульсы всех частиц pi, pk, их
массы mi, т k, энергии
(здесь индексы i, k обозначают и сталкивающиеся ядра
и продукты реакции). Эти величины связаны соотношением
(в системе h = с =1), где р k - четырёхмерный вектор импульса (см. Скорость
четырёхмерная). Они служат основой для выбора кинематич. переменных, наиб.
адекватно описывающих динамич. закономерности процессов. Физически значимой
характеристикой пучков ядер является энергия, приходящаяся на 1 нуклон.
Точно также энергию и импульс участвующих в реакции объектов надо делить на
число составляющих их элементов (конституентов). Отношения импульсов адронов
к их массам выступают в качестве характеристики ср. импульса, приходящегося
на 1 конституент. Вследствие этого процессы в Р. я. ф. описывают в терминах
инвариантных положит. величин (безразмерных):
= 1, то
Здесь индексы a, b могут относиться как к частицам, так и к образующимся
комплексам частиц (кластерам)
Из (2) видно, что
не зависит от
- вероятности процессов для подсистем
Распределения частиц в пространстве 4-скоростей распадаются на кластеры -
группы точек ui, расстояния между к-рыми bik =-(ui- uk)2 значительно меньше
ср. расстояния между всеми точками ансамбля. Изучение кластеризации в
множественном образовании частиц позволило получить релятивистски
инвариантное описание струй- резко направленных выбросов адронной материи
при столкновении частиц и ядер. Согласно существующим представлениям струи
являются продуктами превращения в адроны кварка или глюона, выбитого при
столкновении исходных частиц. Изучение образования струй в столкновениях
ядро - ядро важно для выяснения возможностей квантовой хромодинамики в
описании микроструктуры атомных ядер. Исследование струй показало, что они в
осн. состоят из пи-мезонов. В системе покоя кластера a(ua = 0) кинетич.
энергия пиона составляет 150 МэВ.
можно говорить о столкновениях квазисвободных кварков. Значение
bik, начиная с к-рого реализуются режимы, обусловленные преобладанием
кварковых степеней свободы, определяется условием
> 1,
=
/
10-2.
- энергия связи фрагмента 1 в ядре II, т1.- масса фрагмента, F- слабо
меняющаяся ф-ция. Это соответствует ф-ле (4) при a=I, b=II и n=2. Процессы с
перераспределением нуклонов дают осн. вклад в полное сечение взаимодействия
релятивистских ядер. На рис. 2 приведено распределение по продольному
импульсу p||1. ядер изотопов С, образующегося при столкновении
релятивистских ядер 160 с ядрами Be. Сечения процесса определяются ф-лой
(6); условие
= 0 даёт положение максимумов, а величина
- их ширины. Малость
обусловливает большую величину полного сечения взаимодействия ядер.
Зависимость сечения (6) от
определяет его зависимость от AII. и AI, т. к.
тII= АII т0, mI= = АI т0. При достаточно больших величинах импульсов |pII| и
|pI| величина bII1 зависит только от отношения |pII|/|pI|> т. е. имеет место
инвариантность по отношению к замене импульсов:
где
обычно регистрируются вторичные частицы, вылетающие из мишеней под углом
больше 90° по отношению к направлению пучка ядер (нуклонов, мезонов,
фотонов). Универсальность энер-гетич. и угл. зависимостей образующихся
частиц 1 (пионов, коонов) наблюдалась в широком интервале энергий
столкновения, соответствующих
1 необходимо
условие
при
> 1. Величины
=
являются фундам.
характеристиками каждого ядра, т. к. система кумулятивная частица - ядро
представляет собой, так же, как и кластеры, изолиров. систему. Для случая,
когда поперечный импульс регистрируемой частицы
= 0:
> 1 универсальна для ядер от Не до U (рис. 3, 4).
Величина
= 0,14 и с точностью ~10% одинакова для всех ядер. Постоянство
для
всех изученных ядер и всех
указывает на то, что эта величина является
универсальным параметром ядерной материи.
в
кумулятивной области (
> 1).
определяет возможность
наблюдения явлений, связанных с высвобождением цветных степеней свободы. При
10 образуются барионные кластеры размером, определяемым условием
0,1. Ср.
расстояние между кластерами порядка 1. При
50 формируются струи. Размер
струи4. Струп разделяются, если расстояние между
ними 10. При 200 происходит
множественное образование струй. Область
105 будет достигнута после создания
ядерных коллайдеров. Лит.: Балдин А. М., Физика релятивистских ядер "ЭЧАЯ", 1977, т. 8, № 3, с.
429; Ставинский В С Предельная фрагментация ядер - кумулятивный эффект
(эксперимент), "ЭЧАЯ", 1979, т. 10, № 5, с.949; Efrеmоv А. V Quark-parton
picture of the cumulative production "Progr Part' and Nucl. Phys.", 1981, v.
8, p. 345; Frankfurt L. L., Strikman М. I., High energy Phenomene
Short-Range nuclear structure and QCD, "Phys. Repts", 1981 v. C7B r
216-Вa1din А. М., Study of the nuclei AS quark-gluon systems in relativistic
nuclear collisions, "Nucl. Phys.", 1986, v. A 447 r 203• Вa1din A. M.,
Didenkо L. А., Asymptotic properties of Hadron Matter in relative 4-velocity
space, "Fortschr Phvs." 1990, V. 38, № 4, p. 261. А. M.Балдин.
«Физическая энциклопедия». В 5-ти томах. М.: «Советская энциклопедия», 1988.
РЕЛЯТИВИСТСКАЯ ЯДЕРНАЯ ФИЗИКА
Введение. Традиц. модели ядра как системы нуклонов рассматриваются в рамках
нерелятивистской квантовой механики и описывают эксперим. факты, относящиеся
к невысоким энергиям частиц - не более десятков и сотен МэВ (см. Оболочечная
модель ядра). Релятивистские эффекты при таком подходе являются малыми
поправками. В области относит. скоростей, близких к скорости света с, теория
ядерных процессов становится связанной с решением фундам. проблем теории
квантовых полей. Для описания ядерных взаимодействий при скоростях ядерных
частиц, близких к с, понятие нуклона становится неадекватным, а
протон-нейтронная модель - недостаточной. В качестве составляющих частиц
ядерной материи (квантов) начинают выступать кварки и глюоны, динамика к-рых
определяется ур-ниями квантовой хромодинамики (см. Кварковые модели).
Инвариантные переменные. Характерное явление Р. я. ф.- множественное
рождение частиц (рис. 1).
Рис. 1. Множественное рождение адронов при столкновении релятивистского ядра
углерода с ядром Та (пропановая пузырьковая камера).
где ui, uk- 4-векторы скоростей. Т. к.
В системе покоя одной из частиц, напр. k, bik= 2Ti/mi, где Ti - кинетич.
энергия частицы i в системе покоя частицы k. Если частица k- ядро, то
где m0 = 931 МэВ (~ 1 ГэВ) - атомная единица массы (АБМ). Для взаимодействия
ядер i и k величина bik является кинетич. энергией одного из ядер,
приходящейся на 1 нуклон и выраженной в АЕМ (практически - в ГэВ).
Распределения вероятностей W. (сечения) процессов зависят только от bik и не
зависят от энергии, передачи импульса и т. п. (при фиксированных bik). Это
позволяет воспользоваться методами подобия теории. Помимо соображений
размерности и инвариантности в теории подобия используется гипотеза о том,
что решения (в нашем случае - сечения) обладают асимптотич. поведением. Если
разбить совокупность экспериментально определяемых величин на 2 группы {...bik...}a
и {...bik...}b, то принцип самоподобия (автомодельности) приводит при
достаточно больших a и b к соотношению
(только от xk )и обладает по этой переменной автомо-дельностью. Число n
определяется из теории и измеряется в эксперименте. Из двух параметров
подобия bak и xk только xk является масштабно инвариантным (см. Масштабная
инвариантность).
Важным результатом обобщения эксперим. наблюдений является ослабление
взаимодействия объектов a и b (ядер, адронов, кластеров в пространстве
4-скоро-стей) при увеличении их относит. скорости (при больших bab). Это
свойство может быть записано в виде
где
a и b. Объединение свойств (2) и (3) даёт
Классификация ядерных взаимодействий. Величины bik определяют области
применимости моделей, описывающих механизмы взаимодействия частиц.
Зависимость сечений взаимодействия от bik различна в разных интервалах их
значений. Анализ множественных процессов при столкновениях релятивистских
ядер указывает на существование неск. характерных диапазонов значений bik.
При bik ~ 10-2 можно рассматривать внутриядерное движение нуклонов,
определяемое ср. кинетич. энергией движения нуклонов в ядрах. При 10-2 < bik
< 1 столкновения ядер можно рассматривать как столкновения квазисвободных
нуклонов с распределением по импульсам внутр. движения, задаваемым обычной
ядерной динамикой. При bik ~ 1 следует рассматривать движение связанных
кварков. При 
Это соответствует относит. скоростям частиц u > 0,95 с.
Применение критерия (5) к столкновению ядер I и II даёт величину кинетич.
энергии, необходимой для изучения кварковых степеней свободы. Это означает,
что при энергиях ядер Т >3-4,7Д ГэВ наступает асимптотич. режим, называемый
предельной фрагментацией ядер. В этой области энергий спектр вторичных
частиц (фрагментов ядер, пионов, каонов и т. д.) не зависит от энергии и
сорта налетающей частицы (ядра, адрона, фотона, лептона). Это соответствует
общей закономерности (4) при a = I, b = II.
В области предельной фрагментации ядер обнаружен ядерный кумулятивный
эффект. Он состоит в рождении в неупругих ядро-ядерных (адрон-ядерных)
столкновениях частиц, энергия к-рых превышает максимально возможную для
взаимодействия с отд. нуклонами ядер. Кварковые степени свободы играют
нек-рую роль и в ядерных реакциях при bik< 1 и даже при bik ~ 10-2 в
свойствах осн. состояний ядер. Это связано с тем, что ср. расстояния между
нуклонами в ядре сравнимы с радиусом пленения (конфайн-мента) кварков.
Существует вероятность туннелирова-ния, перемешивания и даже обобществления
кварков, принадлежащих отд. нуклонам. Эксперим. данные по ядерному
кумулятивному эффекту свидетельствуют также о том, что в ядре наряду с
нуклонами возникают "капельки" кварк-глюонной плазмы и что ядра могут
рассматриваться как гетерофазные системы, представляющие собой смесь
нуклонной и кварк-глюонной фаз.
Образование ядерных фрагментов. Реакции с релятивистскими ядрами в области
bI II > 1, но при bII 1 (1 - ядерный фрагмент) или bI1 порядка 10-2
описываются протон-нейтронной моделью ядра. Учёт кварковых степеней свободы
в этой области даёт такие же малые поправки, как и для характеристик
основных и низковозбуждённых состояний ядер. Сечение реакций столкновения
ядер I и II с образованием ядерного фрагмента 1 расщепления ядра II имеет
вид
при 
Здесь 
где l - константа. Эта зависимость отчётливо проявляется в образовании
ядерных фрагментов, a-частиц, дейтронов, протонов (ядерный скейлинг).
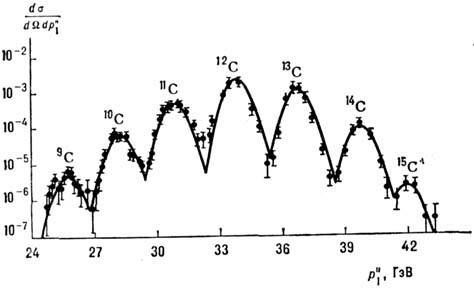
Рис. 2. Зависимость дифференциальных сечений образования изотопов углерода
от их продольного импульса в реакции 16О + Be : С при их энергии ядер
кислорода 2,1 ГэВ (единицы произвольные).
Реакции перераспределения нуклонов между ядерными фрагментами при bII1 ~
10-2-10-1 важны для обнаружения и исследования короткоживущих радионуклидов,
а также для получения пучков нестабильных барионных систем (напр.,
гиперядер). В области 0,1 1 кварковые степени свободы играют существ. роль в
перестройке взаимодействующих адрон-ных систем. Т. к. сечения взаимодействия
здесь относительно большие, то возможны исследования кварковых систем,
отличающихся от обычных трёхкварковых (барионы )или кварк-антикварковых (
мезоны), напр. дибарионных.
Предельная фрагментация ядер. Сечение рождения частицы 1 в области
предельной фрагментации ядра II можно определить исходя из ф-лы (4) при a =
1, b = 2, n =0:
Здесь F1- множитель, слабо зависящий от bI II (т. е. от энергии
столкновения), свойств ядра II и частицы 1;
x1 = bI1/bII1 =
(uz и pz - проекция скорости и импульса на направление пучка). В случае
Представления о динамике образования частиц в области предельной
фрагментации основаны на том, что в столкновениях ядер участвуют их малые
части, несущие доли импульса, равные (XI/АI)pI, (XII/АII)pII.. Эти части (партоны)
могут быть кварками и глюонами. Из законов сохранения энергии-импульса,
записанных в виде
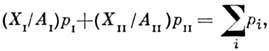
следует, что для предельной фрагментации ядра II при bI II 
Здесь m1 - масса мезона 1. Т. о., XI и ХII- мин. число нуклонов, допускаемое
законами сохранения для образования частицы с заданной величиной x1.
Кумулятивный эффект можно определить как реакции образования частиц,
описываемые ф-лой (7) (т. е. при 
Зависимость (8) при 
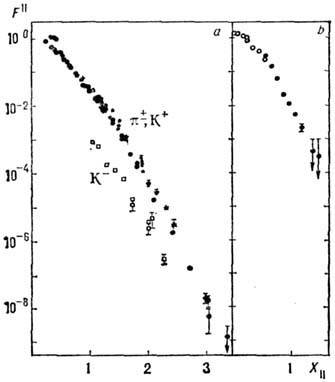
Рис. 3. Зависимость структурной функции ядер от , определённая из сечения
кумулятивного образования p- и К-мезонов в протон-ядерных взаимодействиях.
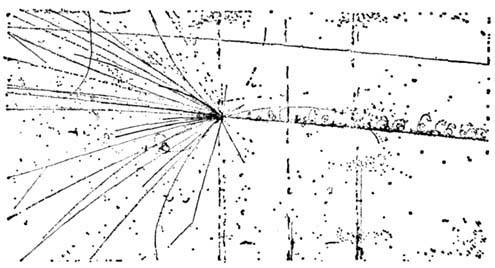
Рис. 4. Зависимость от массового числа А структурной функции ядер
Экспериментальные методы требуют достаточно интенсивных пучков
релятивистских ядер. Для ускорения ядер обычно используют модифициров.
синхротроны протонные. Получение пучков ионов с максимально возможным
зарядом осуществляется либо предварит. ускорением малозарядных ионов,
получаемых от обычных ионных источников с последующей полной "обдиркой"
электронов на твёрдых и газообразных мишенях, либо путём использования спец.
ионных источников, в к-рых образуются "голые" ядра (необходимо для
устойчивого ускорения). Запуск в Дубне ускорителя "Нуклотрон" (1992) в
сочетании с синхрофазотроном даёт возможность ускорения ядер вплоть до U при
высоких пространственно-временных характеристиках пучков.
Для изучения возбуждённых кластеров в пространстве 4-скоростей эффективны
трековые детекторы частиц, позволяющие регистрировать множественное рождение
частиц в условиях 4П-геометрии ( пузырьковые камеры и др.).
Максимальная для данного ускорителя энергия ядер 
(Источник: «Физическая энциклопедия». В 5-ти томах. М.: «Советская
энциклопедия», 1988.)
<< назад
вперед >>
См. также в других словарях:
• ЯДЕРНАЯ ФИЗИКА — раздел физики, посвящённый изучению структуры ат. ядра,
процессов радиоактивного распада и механизма яд. реакций. К Я. ф. иногда
относят также физику элементарных ч ц. Иногда разделами Я. ф. продолжают
считать направления… (Физическая энциклопедия)
• ФЛУКТОН — гипотетич. флуктуация плотности вещества атомного ядра, когда
нуклоны сближаются на расстояние, меньшее их собств. размера. Ф. были
предложены Д. И. Блохинцевым в 1957 для объяснения эффекта интенсивного
квазиупругого выбивания быстрыми… (Физическая энциклопедия)
